Answer:
The times at which the weight is first at a height of 1 cm, of 3 cm, and of 5 cm above the rest position are 78.10s, 61.71s, and 42.41s respectively
Step-by-step explanation:
Given the equation:

Make t the subject:

We now substitute h = 1, 3 and 5
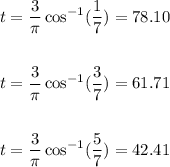
The times at which the weight is first at a height of 1 cm, of 3 cm, and of 5 cm above the rest position are 78.10s, 61.71s, and 42.41s respectively