Question

I need help on these questions number 5,6,7,8,9,10

Answer 1

We are asked to reduce a number of expression with the use of power laws.

First expression is a product of two numbers to the power zero:

`(-3\cdot4)^0`

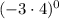
and we know that any real number different from zero to the power zero is "1" (one)

so thw answer for thisis: 1

Second expression:

7 to the power negative 2 times (-3) to the power 2:

We recall that a negative power means that the actual base (in our case the number 7) is on the other side of the fraction line. So, 7 squares is in the denominator.

Also (-3) squared is the product of : (-3) * (-3) which becomes : 9

therefore:

`7^(-2)\cdot(-3)^2=((-3)^2)/(7^2)=(9)/(49)`

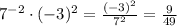
Third expression:

We have a quotient with a to the power -3 in the numerator and b to the power -2 in the denominator. As we said before, the negative in the exponent means that we need to place the expression with positive exponent on the opposite side of the fraction line, so we have b suared now in the numerator, and a cube now in the denominators. Then we replace them by the numbers we are provided: a = 5 and b = 6, and get for answer 36 divided by 125

`(a^(-3))/(b^(-2))=(b^2)/(a^3)=^{}(6^2)/(5^3)=(36)/(125)`

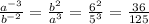
Fourth expression:

`9\cdot x^2\cdot y^(-3)=(9\cdot x^2)/(y^3)=(9\cdot5^2)/(3^3)=(25)/(3)`

Where we applied again the property for negative power, then replace x by 5 and y by 3 as indicated, and at the end simplified common factors of 3 in both numerator and denominator to end up with 25 divided 3.

Fifth expression:

`14\cdot x^(-2)=(14)/(x^2)=(14)/(7^2)=(2)/(7)`

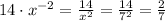
where we replaced x with "7" as required, after we moved the x to the denominator usig the property for negative power. At the end we simplified a factor 7 in numerator and denominator leading to the anser 2/7.