Answer:
The equation is:
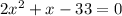
While, the value of
 is:
is:

Explanation:
Step 1: Creating the equation
The area for a rectangle is given by:
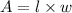
The
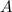 is given as
is given as
 , and
, and
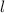 is equal to
is equal to
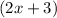 , and
, and
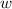 is equal to
is equal to
 .
.
Substitute these values into the formula:
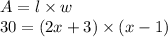
Simplify the equation:

Step 2: Find the value of x
We have the equation as:
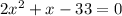
To find the value of
 , we can make use of the quadratic formula:
, we can make use of the quadratic formula:
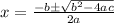
From the equation, we have:
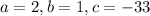
Substitute these values into the formula:
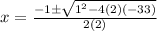
Calculate the values:
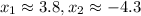
Since using a negative value of
 , can give negative lengths or widths (which is impossible), we will omit it.
, can give negative lengths or widths (which is impossible), we will omit it.
Thus, the value of
 is:
is:
