Question

A 0.050 kg bullet is fired horizontally at 520 m/s and becomes in bedded in the edge of a disk ( M =20 KG, R = 0 .10 M ) that is at rest and free to rotate about its vertical axis. Use moment of inertia for the disc, find the angular velocity of the disc after the collision

Answer 1

Given:

The mass of the bullet, m=0.050 kg

The velocity of the bullet, u=520 m/s

The mass of the disc, M=20 kg

The radius of the disc, R=0.10 m

To find;

The angular velocity of the disc after the collision.

Step-by-step explanation:

From the law of conservation of momentum, the total momentum of a system is always conserved.

Thus,

`mu=(M+m)v`

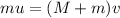
Where v is the linear velocity of the disc after the collision.

On substituting the known values,

`\begin{gathered} 0.050*520=(0.050+20)* v \\ \implies v=(0.050*520)/((0.050+20)) \\ =1.3\text{ m/s} \end{gathered}`

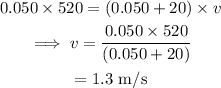
The angular velocity of the disc is given by,

`\omega=(v)/(R)`

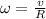
On substituting the known values,

`\begin{gathered} \omega=(1.3)/(0.10) \\ =13\text{ rad/s} \end{gathered}`

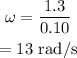
Final answer:

Thus the angular velocity of the disc after the collision is 1