We have to solve this equation:
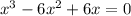
Third degree polynomials like this one are not easily solved, but this one has a root at x = 0. The let us factorize this polynomial as x times a second degree polynomial:
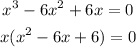
Now we can find the roots of the quadratic polynomial as:
![\begin{gathered} x=\frac{-(-6)\pm\sqrt[]{(-6)^2-4\cdot1\cdot6}}{2\cdot1} \\ x=\frac{6\pm\sqrt[]{36-24}}{2} \\ x=\frac{6\pm\sqrt[]{12}}{2} \\ x=\frac{6\pm\sqrt[]{4\cdot3}}{2} \\ x=\frac{6\pm2\sqrt[]{3}}{2} \\ x=3\pm\sqrt[]{3} \\ x_1=3-\sqrt[]{3} \\ x_2=3+\sqrt[]{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/4czpkopg7youhyvstzd51v2u54y72sluia.png)
Then, the solutions to the equation are:
x = 0
x = 3 - √3
x = 3 + √3