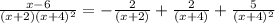-Solution
- In order to solve the question, we need to apply the rule of partial fractions that says:
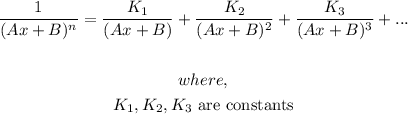
- This rule can be applied to solve the question as follows:
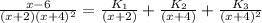
- Cross multiply the denominator on the LHS to remove all denominators
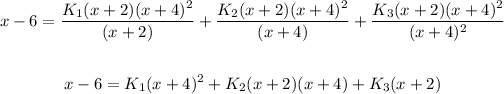
- We can quickly find the values of the constants K1, K2, and K3, if we equate one of the brackets of x to zero. After this, we find the value of x and substitute this value into the equation
- This is done below
![\begin{gathered} (x+4)=0 \\ x=-4 \\ \text{ Substitute x = -4 into the equation} \\ \\ -4-6=K_1(-4+4)^2+K_2(-4+2)(-4+4)+K_3(-4+2) \\ -4-6=K_1(0)+K_2(-2)(0)+K_3(-2) \\ -10=-2K_3 \\ \text{ Divide both sides by -2} \\ \\ K_3=-(10)/(-2) \\ \\ K_3=5 \\ \\ (x+2)=0 \\ x=-2 \\ \text{ Substitute x = -2 into the equation} \\ \\ -2-6=K_1(-2+4)^2+K_2(-2+2)(-2+4)+K_3(-2+2) \\ -8=K_1(2)^2 \\ -8=4K_1 \\ Divide\text{ both sides by 4} \\ K_1=-(8)/(4) \\ \\ \therefore K_1=-2 \\ \\ \text{ Now that we have }K_1\text{ and }K_3,\text{ we can substitute them into the equation and } \\ \text{ find the value of }K_2 \\ \\ x-6=-2(x+4)^2+K_2(x+2)(x+4)+5(x+2) \\ \\ x-6=-2(x^2+8x+16)+K_2(x^2+6x+8)+5x+10 \\ \\ x-6=-2x^2-16x-32+K_2x^2+6K_2x+8K_2+5x+10 \\ \\ Comparing\text{ the coefficients of }x^2\text{ on LHS with the coefficients of }x^2\text{ on the RHS} \\ \\ 0x^2=-2x^2+K_2x^2 \\ 0=-2+K_2 \\ \therefore K_2=2 \end{gathered}]()
- Thus, the breakdown of the rational expression is: