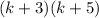Question

Factor k^2 + 8 k + 15

Answer 1

To factor a polynomial of the form:

`k^2+Bk+C`

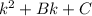
we need to find two integer numbers, a and b, that fullfil the following:

`\begin{gathered} ab=C \\ a+b=B \end{gathered}`

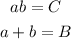
then we write the original polynomial as:

`k^2+ak+bk+C`

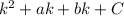
finally we factor by agrupation.

Let's do this with the polynomial:

`k^2+8k+15`

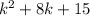
In this case we have that B=8 and C=15. We need two numbers which sum gives 8 and multiplication gives 15; this numbers can be a=5 and b=3, then:

`\begin{gathered} 3\cdot5=15 \\ 3+5=8 \end{gathered}`

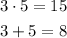
Then we write the polynomial as:

`k^2+5k+3k+15`

and we factor by agrupation:

`\begin{gathered} k^2+8k^2+15=k^2+5k+3k+15 \\ =k(k+5)+3(k+5) \\ =(k+3)(k+5) \end{gathered}`

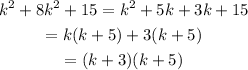
Therefore the factorization of the polynomial is:

`(k+3)(k+5)`