Question

Find the equivalent resistance.Group of answer choices27.5 Ω24.2 Ω18.8 Ω14.9 Ω

Answer 1

We will have the following:

First, we find the equivalent of 15 & 9 ohms, that is:

`(1)/(R)=(1)/(9)+(1)/(15)\Rightarrow\frac{1}{\text{R}}=(8)/(45)\Rightarrow R=(45)/(8)`

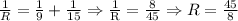
Then, we find the equivalent of R and 8 ohms:

`R_1=8+(45)/(8)\Rightarrow R_1=(109)/(8)`

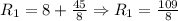
The, we find the equivalent of R1 and 25 ohms:

`(1)/(R_2)=(1)/((109/8))+(1)/(25)\Rightarrow(1)/(R_2)=(309)/(2725)\Rightarrow R_2=(2725)/(309)`

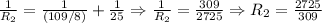
Finally, we calculate the equivalent of R2 and 10 ohms, that is:

`R_3=10+(2725)/(309)\Rightarrow R_3=(5815)/(309)\Rightarrow R_3\approx18.8\Omega`

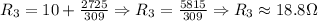
So, the equivalent resistance is approximately 18.8 ohms.