SOLUTION
Write out the function foir the height
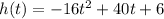
The speed of an object is the rate of change of distance with time. Since rate of change is also differentiation, hence we diferentiate the function above
Applying the rule of differentiation, we have
Recall the rule for diffentiation

hence, we have
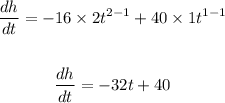
Then the speed of the ball is goven by the function
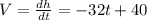
At t= 1, we substitute into the function we obtained for speed
Hence, we have
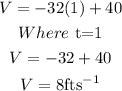
hence
The speed of the ball at t=1s is 8ft/s