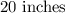Answer:
The approximate diameter of the mirror is;
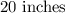
Step-by-step explanation:
Given that the length of ribbon that is enough to go round the circular mirror once is 63 inches which is equal to the circumference of the mirror.
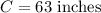
Recall that the formula for the circumference of a circle is;
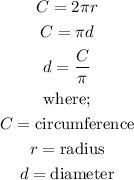
Substituting the value of C to calculate d;
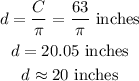
Therefore, the approximate diameter of the mirror is;