Given a quadratic function f(x):

we can find the vertex of the parabolla that represents using the following expression:
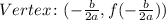
then, in this case, we have the following values for a, b and c:
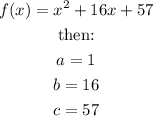
now lets find the x coordinate of the vertex:
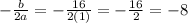
next, to find the y-coordinate of the vertex, we have to evaluate the x-coordinate on the function, that is, we have to find f(-8):
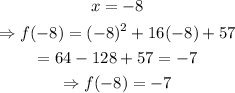
we have that f(-8) = -7, therefore, the vertex of the parabola (and minimum) is located at the point (-8,-7)