Question

For a study, 4 people are chosen at random from a group of 10 people.  How many ways can this be done?

Answer 1

5040 ways

Step-by-step explanation:

If we want to chose 4 people out of a group of 10 people.

Method 1

• We can choose the first person in 10 ways.

,

• We can choose the second person in 9 ways.

,

• We can choose the third person in 8 ways.

,

• We can choose the fourth person in 7 ways.

Therefore, the number of ways this can be done is:

`\begin{gathered} =10*9*8*7 \\ =5040\text{ ways} \end{gathered}`

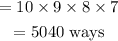
Method 2

We can solve this as a combination problem.

`\begin{gathered} \text{Number of ways=}^(10)C_4 \\ =(10!)/((10-4)!) \\ =(10*9*8*7*6!)/(6!) \\ =10*9*8*7 \\ =5040\text{ ways} \end{gathered}`

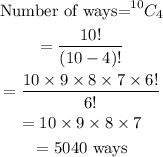
Therefore, the selection can be done in 5040 ways.