It is given that,

The area of the inner circle is calculated as,
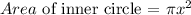
The area of the outer circle is calculated as,
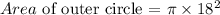
The area of the shaded region is calculated as,
Area of shaded region = Area of the outer circle - Area of the inner circle
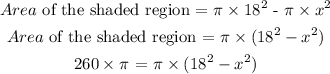
The radius of inner circle is calculated as,
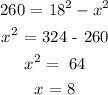
Thus the value of x is 8 cm.