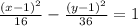Kindly check below
1) For this problem, let's start out with the Ellipse
So, the key features of an Ellipse are:
a,a = (2) Semi-major axis ( the sum of the semi-major axis yields the longer axis of an ellipse), a=6
b,b =(2) Semi-minor axis (the sum of the semi-minor axis yields the shorter axis of an ellipse), b=4
F1, F2 (Foci)=(2√5,0), (-2√5,0)
A1,A2 =(6,0), (-6,0) Vertices (the endpoints of the semi-major axis)
B1, B2 =(4,0), (-4,0) Co-vertices (the endpoints of the semi-minor axis)
Domain: [-6,6] The set of entries of a function, usually represented by x
Range: [-4,4] The set of outputs of a function, usually represented by y
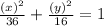
The general formula for an ellipse
2) Now, let's move on to the next conic section. The Hyperbola
In this sketch, we've got the following features:
A_1, A_2: The vertices of a hyperbola are at (5,-1) and (-3,1)
F_1, F_2: Foci of a hyperbola
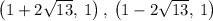
In red: The asymptotes, (in this case slant ones. They set the boundaries where the hyperbola does not trespass.
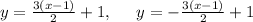
Note that these asymptotes have a slope, so we need to express them as linear equations
P: Generic point on the curve.
Domain: Set of entries of a hyperbola. We can tell that this hyperbola has the following Domain:
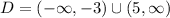
A hyperbola can be given with a general formula as well: