Question

A retailer who sells backpacks estimates that y selling them for x dollars each, he will be able to sell 134 − x backpacks a month.

Answer 1

Given:

`Revenue\text{ function, R\lparen x\rparen= -x}^2+134x`

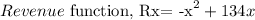
To find the selling price, x, which will give highest revenue, y, we will find maximum value of parabola curve −x² + 134x

The value of -b/2a tells us the value x of the vertex of the function

−x² + 134x

a = -1

b = 134

Thus,

`\begin{gathered} x=-(b)/(2a)=(-134)/(2(-1))\text{ = }(-134)/(-2)\text{ = 67} \\ x=67 \end{gathered}`

The selling price which will give highest revenue= 67 dollars per backpack

R = −x² + 134x

When x = 67

R = −67² + 134(67)

R= -4489 + 8978

R= 4489

Thus, the maximum revenue is 4489 dollars

Summary:

67 dollars per backpack goes into the first box

4489 dollars goes into the second box