We have to predict the number of African cheetahs living in the wild in t = 13 years.
We know that the current population is 7476 and it declines at a rate of 8% per year.
We can express this with an exponential model:
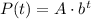
We can find the parameter A knowing that P(0) = 7476.
Then, we will have:
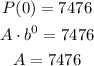
Now, we can use the decrease rate r = 0.08 (or 8%) to find the parameter b.
If the population decrease by 8%, the population after one year will be 8% less. We can express this as:
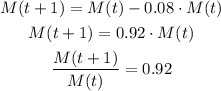
If we replace with the model definition we obtain:
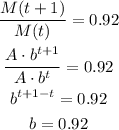
We now have the model for the population after t years:
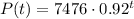
We can now calculate the population after t = 13 years as:
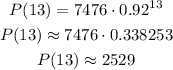
Answer: the number of African cheetahs living in the wild in 13 years is expected to be 2529.