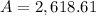Step-by-step explanation:
Given;
We are told that a deposit of $2000 is invested in an account that yields an annual interest of 4.5%, but is compounded monthly.
Required;
We are required to calculate how much money will be in the investment in 6 years time.
Step-by-step solution.
The formula for calculating a compound interest is given as;
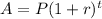
The variables in this formula are;
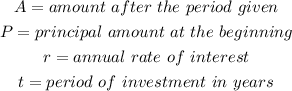
However, when the compounding is done at several periods within a year (for example, monthly, quarterly, half-yearly, etc), the formula is amended to reflect the period of compounding within each year.
The amended formula is what we have been given in this question.
Therefore, from the details provided,
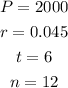
Please note that n is the number of times compounding takes place per year and in this case its 12 times (monthly).
Therefore;
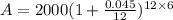

Rounded to the nearest hundredth, we now have
ANSWER: