Answer:
The value of the larger median for the two groups = 7
The value of the larger mean for the two groups = 6.93
The student's in the indoor group are more excited than those in the outdoor group
Explanations:
The median of a data set is the value in the middle of the data set
Median value for the outdoor group = 7
Median value of the indoor group = (5 + 4)/2 = 9/2 = 4.5
The value of the larger median for the two groups = 7
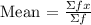
![\begin{gathered} \text{Mean for the indoor group = }((0*1)+(1*1)+(4*1)+(5*3)+(6*4)+(7*5)+(8*6)+(9*6)+(10*2))/(29) \\ \text{Mean = }(0+1+4+15+24+35+48+54+20)/(29) \\ \text{Mean = }(201)/(29) \\ \text{Mean = }6.93 \end{gathered}]()
Mean for the indoor group = 6.93
![\begin{gathered} \text{Mean for the outdoor group = }((0*1)+(1*2)+(2*5)+(3*4)+(4*5)+(5*7)+(6*6)+(7*2)+(8*2))/(34) \\ \text{Mean = }(0+2+10+12+20+35+36+14+16)/(34) \\ \text{Mean = }(145)/(34) \\ \text{Mean = }4.27 \end{gathered}]()
The value of the larger mean for the two groups = 6.93
The difference between the moods of the two groups by comparing their center and shapes
Note that:
The indoor group has a higher mean than the outdoor group
This means that an average student's mood in the indoor group is higher than that of the student in the outdoor group.
This means that the students in the indoor group are more excited than the outdoor group