Question

Points z1 and z2 are shown on the graph.Part A: Identify the points in standard form and find the distance between them.Part B: Give the complex conjugate of z2 and explain how to find it geometrically.Part C: Find z2 − z1 geometrically and explain your steps.

Answer 1

Given

Points on a graph.

Find

a) identify the points and find the distance between them.

b) complex conjugate of second point.

c) find z2 - z1

Step-by-step explanation

a) as we see from the graph , points are

`\begin{gathered} z_1=(3,5) \\ z_2=(6,-3) \end{gathered}`

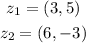
distance is given by

`\begin{gathered} √((x_2-x_1)^2+(y_2-y_1)^2) \\ √((6-3)^2+(-3-5)^2) \\ √(3^2+(-8)^2) \\ √(9+64) \\ √(73) \end{gathered}`

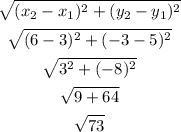
b) Conjugate of z2

as we have ,

`z_2=6-3i`

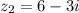
so , conjugate is given by

`z_2=6+3i`

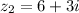
c) we have ,

`\begin{gathered} z_1=3+5i \\ z_2=6-3i \end{gathered}`

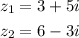
so ,

`\begin{gathered} z_2-z_1=(6-3i)-(3+5i) \\ z_2-z_1=6-3i-3-5i \\ z_2-z_1=3-8i \end{gathered}`

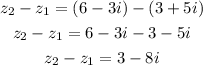
Final Answer

Hence , the required answers are

a) distance =

`√(73)`

b) conjugate = 6 + 3i

c) 3 - 8i