Question

The circle graph shows how the annual budget for a company is divided by department. Use this graph to answer the questions below.(a) Which department gets approximately one-fourth of theannual budget?Select OneSupportEngineeringMediaEditorialResearch(b) Approximately what percentage of the budget goes toEngineering and Support combined?20% O 40%60%80%SalesХ5?

Answer 1

Observe the given graph carefully.

In a circle graph, the circle is divided into different sectors, each characterized by its central angle.

The complete circle measures 360 degrees. So the complete distribution (100% data) corresponds to 360 degrees.

In the given problem, we are concerned with the budget,

`360^(\circ)=100\text{ percent budget}`

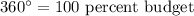
(a)

Consider the following,

`\begin{gathered} \text{ Total budget}=360^(\circ) \\ (1)/(4)*\text{ Total budget}=(1)/(4)*360^(\circ)=90^(\circ) \end{gathered}`

So, one-fourth of the budget will correspond to the department which covers the 90-degree sector of the circle graph.

As observed from the graph, the most suitable department under this criteria is the Engineering Department.

Thus, Engineering Department gets approximately one-fourth of the annual budget.

(b)

Consider that the departments Engineering and support combiningly cover a little more than one-third of the area of complete circle.

Consider the following,

`\begin{gathered} 360^(\circ)=100\text{ percent} \\ 120^(\circ)=(120)/(360)*100=33.33\text{ percent} \end{gathered}`

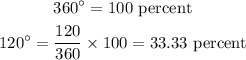
Note that the area covered by the department is a little more than one-third, so the corresponding percentage value must also be a little more than 33.33%.

From the available options, 40% is the value available next to 33.33%, so this should be the most suitable choice.

Thus, it can be concluded that approximately 40% of the annual budget goes to the departments Engineering and Support combined.

Therefore, option (b) is the correct choice.