ANSWER
The heat of formation of propane is -195KJ
Step-by-step explanation
Given that;
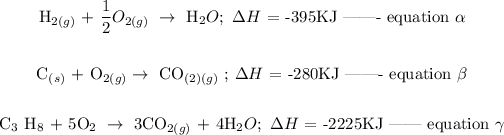
Follow the steps below to find the heat of formation of propane
Step 1; multiply equation alpha by 4
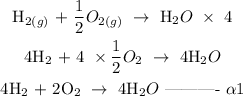
Step 2; multiply equation beta by 3
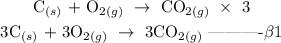
Step 3; Reverse the equation gamma
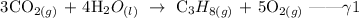
Step 4; Add equation alpha1, beta1, and gamma1 together
![\begin{gathered} \text{ 4H}_(2(g))\text{ + 2O}_(2(g))_\text{ + 3O}_(2(g))+\text{ 3C}_((s))\text{ + 3CO}_(2(g))\text{ + 4H}_2O(l)\text{ }\rightarrow\text{ 4H}_2O(l)\text{ + 3CO}_(2(g))\text{ + 5O}_(2(g))\text{ + C}_3H_(8(g)) \\ \text{ 4H}_(2(g))\text{ + 5O}_(2(g))\text{ + 3C}_((s))\text{ + 3CO}_(2(g))\text{ + 4H}_2O(l)\text{ }\rightarrow\text{ 4H}_2O(l)\text{ + 3CO}_(2(g))\text{ + 5O}_(2(g))\text{ + C}_3H_(8(g)) \\ \text{ 4H}_(2(g))+\cancel{5O_2}+\cancel{3CO_2}+\cancel{4H_2}O\text{ + 3C}\rightarrow\cancel{4H_2}O+\cancel{3CO_2}+\cancel{5O_2}\text{ + C}_3H_8 \\ \text{ 4H}_(2(g))\text{ + 3C}_((s))\text{ }\rightarrow\text{ C}_3H_(8(g)) \\ \end{gathered}]()
Step 5 ; Evaluate the heat of formation of propane
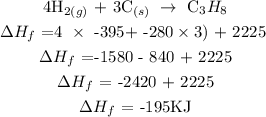
Therefore, the heat of formation of propane is -195KJ