We can divide the surface of the pyramid into the following shapes:
and
In order to determine the surface area, we have to add the areas of all this shapes. That is, the area of 4 triangles and a square.
The area of a triangle is given by
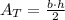
where b is the lenght of the base and h is the lenght of its height.
The area of a square is given by
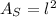
where l is the lenght of its side.
So, in order to determine the surface area of the pyramid, we need to get:
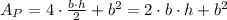
since the sides of the squares are the bases of the triangles.
Using the data we have:
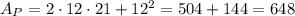
Thus, the surface area of the pyramid is 648 square units.