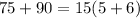We need to find the greatest common factor GCF of the two numbers, then first list the prime factors of each number:
a. 28: 2*2*7
42: 2*3*7
28 and 42 share one 2 and one 7 in common.
Multiply it to get the GCF: 2*7=14.
The GCF of 28 and 42 is 14.
Now, to use the distributive property, write the sum in the form: GCF(a+b) then:
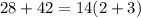
b. 40+25
40: 2*2*2*5
25: 5*5
They share one 5 in common.
The GCF of 40 and 25 is 5.
By using the distributive property:
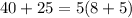
c. 30+54
30: 2*3*5
54: 2*3*3*3
They have one 2 and one 3 in common. Then 2*3=6.
The GCF of 30 and 54 is 6.
By using the distributive property:
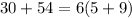
d. 75+90
75: 3*5*5
90: 2*3*3*5
They have one 3 and one 5 in common. So 3*5=15.
The GCF of 75 and 90 is 15.
By using the distributive property: