Answer:
The expression is given below as
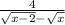
Concept:
To rationalize the denominator, we will multiply by the conjugate given below
The conjugate is given below as
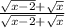
Step 1:
Multiply the expression in the question by the conjugate, we will have
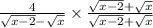
By expanding the brackets, we will have
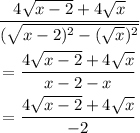
Step 2:
Factor our the common number and divide
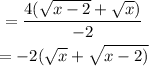
Hence,
The final answer is
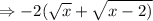
OPTION A is the right answer