Make a diagram to visualize the problem.
As you can observe, at point A the roller-coater has both mechanical energies, while at point B, it has just potential energy because it stops once reaches the 24-meters hill.
Using the law of conservation of energy, we have'
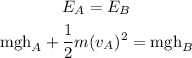
We can cancel out because they are the same, and solve for v_A.
![\begin{gathered} gh_A+(1)/(2)v^2_A=gh_B \\ (1)/(2)v^2_A=gh_B-gh_A \\ v^2_A=2(gh_B-gh_A) \\ v_A=\sqrt[]{2(gh_B-gh_A)} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/skezncei1h69ejrq6jj805b2bnhx8dtv1f.png)
Where g = 9.8 m/s^2, h_B = 24 m, and h_A = 11 m.
![\begin{gathered} v_A=\sqrt[]{2(9.8\cdot24-9.8\cdot11)}((m)/(s)) \\ v_A=\sqrt[]{2(235.2-107.8)}((m)/(s)) \\ v_A\approx16((m)/(s)) \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/7kbep0fdz2mxpc6lcyvc3olotqezgcq6ca.png)
Therefore, the minimum velocity the roller-coaster would need when going over the 11-meters hill is 16 m/s.