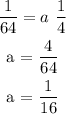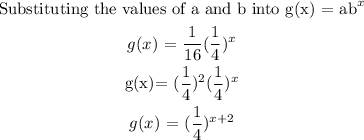Question

The question is in the pic, I just need the answer

Answer 1

Answer:
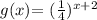
`g(x)\text{= (}(1)/(4))^(x+2)`Explanations:

An exponential function is given by the equation:

`y=ab^x`

For the points (-2, 1) and (1, 1/64)

`x_1=-2,y_1=1,x_2=1,y_2=(1)/(64)`

Substitute x₁, y₁, x₂, and y₂ into the functions to form two equations

`\begin{gathered} y_1=ab^(x_1) \\ y_2=ab^(x_2) \end{gathered}`
`\begin{gathered} \text{1 = }ab^(-2)\ldots\ldots(1) \\ (1)/(64)=ab^1\ldots\ldots.(2) \end{gathered}`

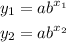
Divide equation (2) by equation (1)

`\begin{gathered} (1)/(64)=\text{ }(ab^1)/(ab^(-2)) \\ (1)/(64)=b^3 \\ b\text{ = }\frac{1}{\sqrt[3]{64}} \\ \text{b = }(1)/(4) \end{gathered}`

Substitute the value b = 1/4 into the equation (2)

`\begin{gathered} (1)/(64)=a\text{ }(1)/(4) \\ \text{a = }(4)/(64) \\ \text{a = }(1)/(16) \end{gathered}`
`\begin{gathered} \text{Substituting the values of a and b into g(x) = ab}^x \\ g(x)\text{ = }(1)/(16)((1)/(4))^x \\ \text{g(x)= (}(1)/(4))^2((1)/(4))^x \\ g(x)\text{ = (}(1)/(4))^(x+2) \end{gathered}`