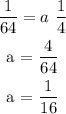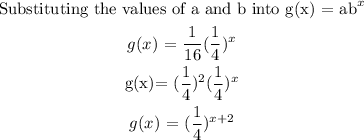Answer:
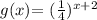
Explanations:
An exponential function is given by the equation:
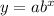
For the points (-2, 1) and (1, 1/64)
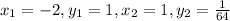
Substitute x₁, y₁, x₂, and y₂ into the functions to form two equations
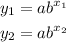
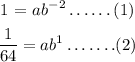
Divide equation (2) by equation (1)
![\begin{gathered} (1)/(64)=\text{ }(ab^1)/(ab^(-2)) \\ (1)/(64)=b^3 \\ b\text{ = }\frac{1}{\sqrt[3]{64}} \\ \text{b = }(1)/(4) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/dcf657rt7aawc4w3iioxcf2y2sn07uzp2r.png)
Substitute the value b = 1/4 into the equation (2)