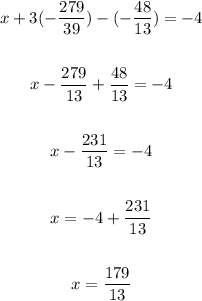Question

Solve the system of equations:x + 3y - z = -4 2x - y + 2z = 13 3x - 2y - z = -9

Answer 1

The solution to the system of equations is

`\begin{gathered} x=(179)/(13) \\ \\ y=-(279)/(39) \\ \\ z=-(48)/(13) \end{gathered}`

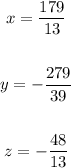
Step-by-step explanation:

Giving the system of equations:

`\begin{gathered} x+3y-z=-4\ldots\ldots\ldots\ldots\ldots\ldots..........\ldots\ldots\ldots\ldots.\ldots\text{.}\mathrm{}(1) \\ 2x-y+2z=13\ldots\ldots...\ldots\ldots\ldots\ldots..\ldots..\ldots\ldots\ldots\ldots\ldots.(2) \\ 3x-2y-z=-9\ldots\ldots\ldots.\ldots\ldots\ldots\ldots....\ldots\ldots.\ldots\ldots\ldots\text{.}\mathrm{}(3) \end{gathered}`

To solve this, we need to first of all eliminate one variable from any two of the equations.

Subtracting (2) from twice of (1), we have:

`5y-4z=-21\ldots\ldots\ldots\ldots\ldots.\ldots.\ldots..\ldots..\ldots\ldots.\ldots..\ldots\text{...}\mathrm{}(4)`

Subtracting (3) from 3 times (1), we have

`3y-5z=-3\ldots\ldots...\ldots\ldots..\ldots\ldots\ldots\ldots\ldots.\ldots\ldots\ldots\ldots\ldots..\ldots\ldots(5)`

From (4) and (5), we can solve for y and z.

Subtract 5 times (5) from 3 times (4)

`\begin{gathered} 13z=-48 \\ \\ z=-(48)/(13) \end{gathered}`

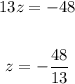
Using the value of z obtained in (5), we have

`\begin{gathered} 3y-5(-(48)/(13))=-3 \\ \\ 3y+(240)/(13)=-3 \\ \\ 3y=-3-(240)/(13) \\ \\ 3y=-(279)/(13) \\ \\ y=-(279)/(39) \end{gathered}`

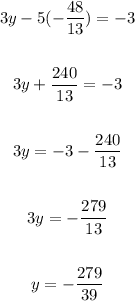
Using the values obtained for y and z in (1), we have

`\begin{gathered} x+3(-(279)/(39))-(-(48)/(13))=-4 \\ \\ x-(279)/(13)+(48)/(13)=-4 \\ \\ x-(231)/(13)=-4 \\ \\ x=-4+(231)/(13) \\ \\ x=(179)/(13) \end{gathered}`