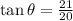ANSWERS
a.
b. sin(θ) = 21/29
c. tan(θ) = 21/20
Step-by-step explanation
For any right triangle the trigonometric ratios are:
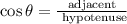
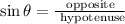
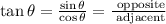
We know the hypotenuse and the adjacent, we want to know the opposite. We can find it using the Pythagorean theorem:
![\begin{gathered} h^2=(\text{adjacent)}^2+(\text{opposite)}^2 \\ 29^2=20^2+(\text{opposite)}^2 \\ \text{opposite}=\sqrt[]{29^2-20^2} \\ \text{opposite}=\sqrt[]{441} \\ \text{opposite}=21 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/k59phh5290g431y2ge5z405a4s9y59q4bu.png)
The sine of the angle is:
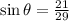
The tangent is: