The figure attached is composed of a cylinder and an sphere. Then:
Surface Area = Total Area of the Sphere + Side Area of the Cylinder.
Hence:
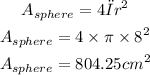
Now, the side area of the cylinder:
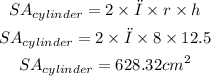
Finally:
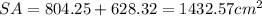
ANSWER
The surface area is 1432.6 cm²
Now, to find the volume:
Total Volume = Volume of the Sphere + Volume of the Cylinder
Volume of the Sphere:
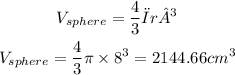
Volume of the Cylinder:
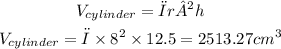
Finally:
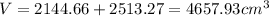
ANSWER
The volume is 4657.9cm³