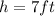Question

The gable end of the root shown is divided in half by a vertical brace. The vertical distance h in fr from an eave to the peak

Answer 1

Step 1. Form a right triangle using the 25 ft length, h, and half of the horizontal length:

Step 2. Since the whole horizontal length is 48ft, half of it is equal to:

`(48ft)/(2)=24ft`

Thus, we have that one leg of the triangle is h, and the other is 24 ft:

Step 3. The red triangle we have is a right triangle, and thus, we can use the Pythagorean theorem to find h.

The Pythagorean theorem for a right triangle is:

`(leg1)^2+(leg2)^2=(hypotenuse)^2`

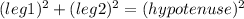
In this case, the hypotenuse is the 25 ft length:

`\text{hypotenuse}=25ft`

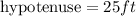
We will label the 24 ft length as leg 1, and h as leg 2:

`\begin{gathered} \text{leg}1=24ft \\ \text{leg}2=h \end{gathered}`

Substituting in the Pythagorean theorem:

`(24ft)^2+h^2=(25ft)^2`

Step 4. Solve for h in the previous equation.

To solve for h, first, we solve the operations:

`576^{}ft^2+h^2=625ft^2`

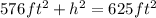
Subtract 576ft^2 to both sides:

`\begin{gathered} h^2=625ft^2-576ft^2 \\ h^2=49ft^2 \end{gathered}`

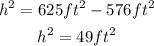
Finally, take the square root of both sides of the equation:

`\begin{gathered} \sqrt[]{h^2}=\sqrt[]{49ft^2} \\ h=7ft \end{gathered}`

We have found the answer for the value of h.

Answer:

`h=7ft`