Question

The arm in the figure below weighs 42.3 N. The force of gravity acting on the arm acts through point A. Determine the magnitude of the tension force FT in the deltoid muscle of the force FS exerted by the shoulder on the humerus to hold arm in the position shown. Find Ft and Fs.

Answer 1

Given:

Weight of arm = 42.3 N

Let's determine the magnitude of the tension force in the deltoid muscle force exerted by the shoulder.

Here, we are to find Ft and Fs.

To solve for Ft, take the equation for the sum of forces about point O.

We have:

`F_t*0.080sin12-42.3*0.290=0`

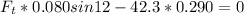
Rewrite the equation for Ft and evaluate:

`\begin{gathered} F_t*0.016633-12.267=0 \\ \\ F_t=(12.267)/(0.016633) \\ \\ F_t=737.51\text{ N} \end{gathered}`

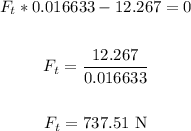
Therefore, Ft = 737.51 N

Now, for the sum of vertical forces, we have:

`\begin{gathered} -42.3+737.51*sin(12)-F_s*sin(\theta)=0 \\ \\ F_ssin(\theta)=-42.3+737.51sin(12) \\ \\ F_ssin(\theta)=115.20\text{ N} \end{gathered}`

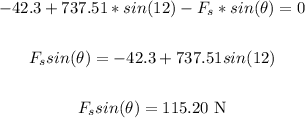
• For the sum of horizontal forces, we have:

`\begin{gathered} F_scos(\theta)-F_tcos(12)=0 \\ \\ F_scos(\theta)=F_tcos(12) \\ \\ F_scos(\theta)=737.51cos(12) \\ \\ F_scos(\theta)=721.39\text{ N} \end{gathered}`

Now, we have the equations:

`\begin{gathered} F_ssin(\theta)=115.20\text{ N} \\ F_scos(\theta)=721.39\text{ N} \end{gathered}`

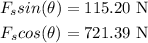
Combine both equations:

`F_ssin(\theta)+F_scos(\theta)=115.20+721.39`

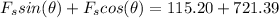
Square all terms:

`\begin{gathered} F_s^2sin^2(\theta)+F_s^2cos^2(\theta)=115.20^2+721.39^2 \\ \\ Fs^2(sin^2(\theta)+cos^2(\theta))=115.20^2+721.39^2 \\ \\ \text{ WHere:} \\ (sin^2(\theta)+cos^2(\theta))=1 \end{gathered}`

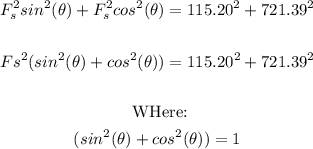
Solving further:

`\begin{gathered} F_s^2*1=115.20^2+721.39^2 \\ \\ F_s^2=533674.5721 \end{gathered}`

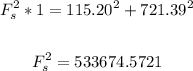
Take the square root of both sides:

`\begin{gathered} √(F_s^2)=√(533674.5721) \\ \\ F_s=730.53\text{ N} \end{gathered}`

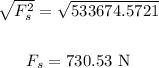
ANSWER:

• Ft = 737.51 N

,

• Fs = 730.53 N