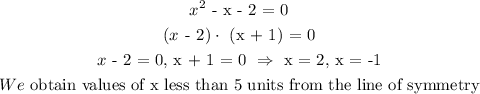line of symmetry is x = 1
a = 1;

Condition: the x-intercepts are less than5 units from the stated line of symmetry
Line of symmetry is given by the formula: x = -b/2a
Remember that x = 1, a = 1
substitute into the formula for the line of symmetry
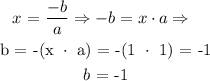
Condition: the x-intercepts are less than5 units from the stated line of symmetry