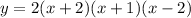Question

Given the points (-2, 0), (-1,0), (0, – 8), (2, 0), write the polynomial in factored form.

Answer 1

As per given by the question,

There are given that four point.

The point is,

`(-2,\text{ 0), (-1, 0), (0, -8), (2, 0)}`

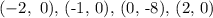
Now,

From given point,

`(-2,\text{ 0), (-1, 0), (0, -8), (2, 0)}`

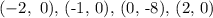
Then, the factor is,

`(x+2)(x+1)(x-2)`

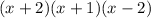
Now, solve the above equation,

`(x+2)(x+1)(x-2)`

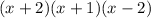
The factorial formd will be,

`y=a*(x+2)*(x+1)*(x-2)`

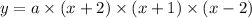
Now, find the value of "a" with the help of given point (0, -8).

So,

Puth the value of x =0, and y=-8 in above equation,

Then,

`\begin{gathered} y=a*(x+2)*(x+1)*(x-2) \\ -8=a*(0+2)*(0+1)*(0-2) \\ -8=a(2)(1)(-2) \\ a=(-8)/(-4) \end{gathered}`

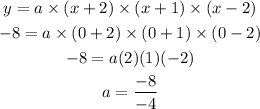
Then, a=2.

Now,

The value of a is 2.

And,

The polynomial in the factored form is,

`y=2(x+2)(x+1)(x-2)`

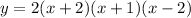
Hence, the value of a is 2 and the polynomial in the factored form is,

`y=2(x+2)(x+1)(x-2)_{}`