So, let's start with setting u to the part inside the sine:
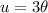
This makes the equations simpler:

For the interval [0, 2π), the sine function will normally have two possible angles for it, but not for the cases sin(u) = 1 and -1. In these, we will have only one possible angle.
In the unit circle, we can see that it is:
So,
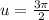
For the interval [0, 2π).
Each complete rotation around the circle, we will get to this place again, and we can do any number of rotations. Each rotation add or substract 2π, so the general solution is:
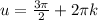
Now, to get these solutions for θ, we can simply substitute it back.
For the solution in [0, 2π):
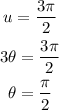
And for the general solution, we have:

Summarizing, we have the answers:
1 - u in [0, 2π):
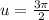
2 - u general:
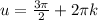
3 - θ in [0, 2π):
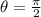
4 - θ general:
