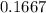Solution:
The probability of an event is expressed as
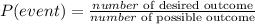
Given:
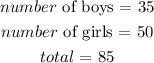
This implies that the number of possible outcomes is 85.
Since two boys are chosen, the selection is thus without replacement.
The probability that the chosen two are boys is expressed as
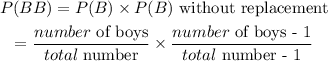
Thus, we have
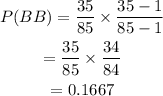
Hence, the probability that both will be boys is evaluated to be