Question

11) () Identify the verten, is of symmetry, and minim ve 54241

Answer 1

The given function is

`f(x)=-(4)/(5)x^2+(48)/(5)x-(114)/(5)`

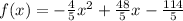
First, we find the vertex V(h,k), where

`h=-(b)/(2a)`

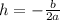
a = -4/50 and b = 48/5.

`\begin{gathered} h=-((48)/(5))/(2(-(4)/(5)))=((48)/(5))/((8)/(5))=(48)/(8) \\ h=6 \end{gathered}`

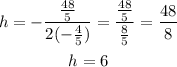
Then, we find k by evaluating the function for x = 6.

`\begin{gathered} f(6)=-(4)/(5)(6)^2+(48)/(5)(6)-(114)/(5)=-(4)/(5)\cdot36+(288)/(5)-(114)/(5) \\ f(6)=-(144)/(5)+(288)/(5)-(114)/(5)=(-144+288-144)/(5)=(0)/(5)=0 \end{gathered}`

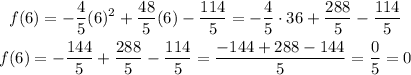
Hence, the vertex is (6,0).

The axis of symmetry is given by h, so it's x = 6.

The maximum value is given by k, so it's y = 0.