Question

The weight limit at a weigh station for an 18-wheeler is 40 tons, which includes the weight of the truck and all material on-board. Jack is driving an 18-wheeler (with trailer) that weighs about 32,000 pounds without any cargo on board. He is hauling market pigs this week. If the average weight of a market pig is 250 pounds, about how many pigs can Jack carry on the 18-wheeler and stay within the weight regulations? (1T = 2000lbs)

Answer 1

From the question, we have the following information:

1. The weight limit for an 18-wheeler is 40 tons (weight of the truck + all material on board).

2. The 18-wheeler that Jack is driving weighs about 32,000 pounds (without any cargo onboard).

3. The average weight of a market pig is 250 pounds.

To solve this problem, we have that the conversion factor is 1T = 2000lbs, and we need to convert the given values into Tons to find the number of pigs that Jack can carry on the 18-wheeler.

Case: 18-wheeler ---> 32,000 pounds. We need to make the conversion into Tons. Then, we have:

`32000lbs\cdot\frac{1T}{2000\text{lbs}}=16T`

Case: the weight of the pigs ---> 250 pounds:

`250\text{lbs}\cdot\frac{1T}{2000\text{lbs}}=0.125T`

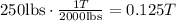
And now, we have that we have 40T - 16T = 24T (available to have as a cargo).

If we have that each pig weighs 0.125T, then, we can represent this situation as follows:

`0.125x=24`

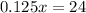
To solve this equation, we can divide both sides of it by 0.125 (division property of equality):

`(0.125)/(0.125)x=(24)/(0.125)\Rightarrow x=192`

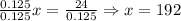
Then, we have that Jack can carry as many as 192 pigs (if they weigh 250 pounds on average) as cargo, and staying within the weight regulations.