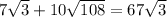We need to use the following property of radicals to solve this question:
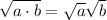
The expression given is:
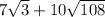
If we want to simplify, we need to rewrite the second term in terms of sqrt(3). We know that 108 is divisible by 3 because the sum of its digits is also divisible by 3.
Then:
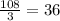
We can rewrite:
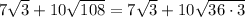
Using the property above:
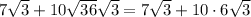
Now, we can simplify:
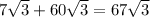
Thus, the answer is: