Question

(b) How much would you need to sell for option A to produce a larger income? Showyour work.

Answer 1

Given:

• Option A:

Base salary = $34,000

Commission on sales = 12% ==> 0.12

• Option B:

Base salary = $40,000

Commission on slaes = 5% ==> 0.05

Let's find how much you need to sell for option A to produce a larger income.

For option A, we have the equation:

y = 0.12x + 34000

For option B, we have the equation:

y = 0.05x + 40000

Where x represents the amount of sales made.

To find how much you need to sell for option A to produce a larger income, set the expression in A to be greater than that of B. Then solve for x.

0.12x + 34000 > 0.05x + 40000

0.12x - 0.05x > 40000 - 34000

0.07x > 6000

Divide both sides by 0.07:

`\begin{gathered} (0.07x)/(0.07)>(6000)/(0.07) \\ \\ x>85714.3 \end{gathered}`

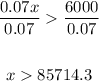
Therefore, you will need to make a minimum of $85715 sales to for option A to roduce a larger income.

ANSWER:

85715