1 Answer

William Yang · Answer 1 · 2023-02-12T19:54:47+0000

Step 1: Sum of angle in a triangle =180

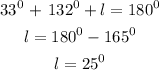
$\begin{gathered} 33^0\text{ + 132}^0+l=180^0 \\ l=180^0-165^0 \\ l=25^0 \end{gathered}$

Step 2: Find the value of m using the sine rule

Sine rule is given as

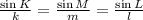
$(\sin K)/(k)=(\sin M)/(m)=(\sin L)/(l)$

k= 1.1 inches

K = 33°

M = 136°

L = 25°

After substitution we will have

$\begin{gathered} (\sin33)/(1.1)=(\sin136)/(m) \\ m\sin 33\text{ = 1.1sin136} \\ 0.54464m=0.76412 \\ m\text{ =1.4inches} \end{gathered}$

Step 3

Find l using sine rule

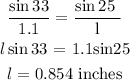
$\begin{gathered} (\sin33)/(1.1)=\frac{\sin 25\text{ }}{\text{l}} \\ l\sin 33\text{ = 1.1sin25} \\ l=0.854\text{ inches} \end{gathered}$

Step 4

Find the area of the triangle using heroin's formula stated as

$\begin{gathered} A=\sqrt[]{s(s-a)(s-b)(s-c)_{}} \\ \text{where s, the semiperimeter}=(a+b+c)/(2) \end{gathered}$

Where

a= k =1.1 inches

b = m = 1.4 inches

c = l =0.854 inches

Substituting these in

Hence the area of 0.5 square inches

Please log in or register to add a comment.