Question

which graph shows the dilation image of rectangle ABCD with the center of dilation at the origin and a scale factor of 1/3

Answer 1

To dilate an image with the dilation center at the origin, you have to multiply the coordinates of each vertex by the dilation factor k, you can write the rule as:

`(x,y)\to(kx,ky)`

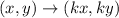
• If the dilation factor is greater than 1, ,k > 1,, then the dilation will be an ,enlargement,, and the resulting shape will be greater than the original.

,

• If the dilation factor is less than 1, ,k < 1,, then the dilation will be a reduction, and the resulting shape will be ,smaller ,than the original.

The rectangle ABCD was dilated using a scale factor k=1/3.

The scale factor is less than one, so the dilation will be a reduction and the image will be smaller than the preimage.

To determine the dilation you can calculate it, first determine the coordinates of each vertex of rectangle ABCD

A(-3,0)

B(0,-3)

C(3,0)

D(0,3)

Next, multiply each coordinate by the scale factor to determine the coordinates of the dilated rectangle A'B'C'D'

A(-3,0) → A'(1*3*(-3),1/3*0)=A'(-1,0)

B(0,-3) → B'(1/3*0,1/3*(-3))=B'(0,-1)

C(3,0) → C'(1/3*3,1/3*0)=C'(1,0)

D(0,3) → D'(1/3*0,1/3*3)=D'(0,1)

So the coordinates of the rectangle A'B'C'D' are

A'(-1,0)

B'(0,-1)

C'(1,0)

D'(0,1)

And the graph that corresponds to a dilation using scale factor 1/3 of the given quadrilateral is the second one (the smaller image).