The exact answer in simplest form for the area of the sector is 2.258π square miles.
To find the area of a sector, you can use the formula:
Area of Sector=
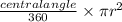
where:
Central Angle is the angle in degrees of the sector,
π is a mathematical constant approximately equal to 3.14159,
r is the radius of the circle.
In this case, the radius (r) is given as 3 kilometers, and the central angle is 120°.
Area of Sector=
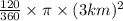
Now, calculate the area:
Area of Sector=
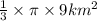
Area of Sector=3πkm^2
Now, you mentioned the answer should be in square miles. To convert square kilometers to square miles, you can use the conversion factor: 1 square kilometer = 0.239 square miles.
Area of Sector in square miles=3π×0.239mi^2
Now, calculate the numerical value:
Area of Sector in square miles≈2.258πmi^2
So, the exact answer in simplest form for the area of the sector is 2.258π square miles.