Given:
The number of students who like orange soda is n(O) = 22.
The number of students like Pepsi is n(P) = 34.
The number of students who like coke is n(C) = 20.
The number of students who like grapes is n(G) = 29.
The objective is to like the number of students like coke is 500 students are surveyed.
Step-by-step explanation:
The total number of students surveyed initially is,
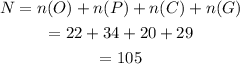
Then, the ratio of number of students who like coke is,

If 500 students are surveyed, the ratio of coke will be,
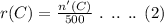
Here, n'(C) represents the number of students who like coke when 500 students are surveyed.
To find n'(C):
On equating both equations (1) and (2),
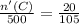
On further solving the above equation,
![undefined]()