Question

Solve for the unknown in the following diagram. Round all answers to two decimal places. cm

Answer 1

The Law of Sines

It's a formula that relates side lengths to their opposite angle measure.

We are given a triangle ABC where one of its sides is AC=52.6 cm. Angles A and C are also known, A=44°, C=100°.

We can calculate the third angle by subtracting A+C from 180°:

B = 180° - 44° - 100° = 36°

Now we calculate the side length x by using the law of sines as follows:

`(52.6)/(\sin 36)=(x)/(\sin 44\~)`

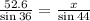
Solving for x:

`x=52.6\cdot(\sin 44)/(\sin 36)`

Calculating:

Thus x = 62.17 cm