Question

Please help me with this it is a practice but I want to prepare for an upcoming test I have. I would really appreciate a good explanation :)

Answer 1

The circle equation is given by

`(x-h)^2+(y-k)^2=r^2`

where the center is at point (h,k) and the radius is r.

For circle O, we get

`\begin{gathered} (x+2)^2+(y-7)^2=5^2 \\ (x+2)^2+(y-7)^2=25 \end{gathered}`

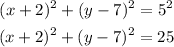
and for circle P, we have

`\begin{gathered} (x-12)^2+(y+1)^2=12^2 \\ (x-12)^2+(y+1)^2=144 \end{gathered}`

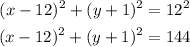
Now, in order to obtain circle P from circle O, we need 2 translations and 1 expansion, that is,

we must translate the center of circle O at (-2,7) 14 units right and 8 units down and get the center of circle P at (12,-1).

These translatiions are given by

`\begin{gathered} (h,k)\Rightarrow(h+14,k) \\ \text{and} \\ (h+14,k)\Rightarrow(h+14,k-8) \end{gathered}`

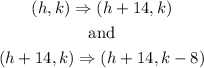
where (h,k)=(-2,7). By doing these tranlastions, we get

Finally, in order to get the circle P, we need to stretch the radius from r=5 to r=12, this transformation is given by

`r=5\Rightarrow r=12`

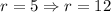
which give us circle P (blue circle in the last picture)