Question

WXYZ is a rectangle if M angle w x y equals 6X squared - 6 find a

Answer 1

Given the rectangle WXYZ, the angle m∠WXY=6a²-6

The given angle is a corner angle, and as you might remember all corner angles of a rectangle are right angles, so we can say that the given expression equals 90 degrees:

`6a^2-6=90`

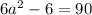
From this expression you can calculate the value of a.

First step is to add 6 to both sides of the equation so that the a-related term stays alone in the left side of the equation and all costants are in the other side:

`\begin{gathered} 6a^2-6+6=90+6 \\ 6a^2=96 \end{gathered}`

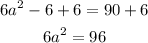
Next divide both sides by 6:

`\begin{gathered} (6a^2)/(6)=(96)/(6) \\ a^2=16 \end{gathered}`

And calculate the square to both sides of the variable to reach the possible value of a:

`\begin{gathered} \sqrt[]{a^2}=\sqrt[]{16} \\ a=4 \end{gathered}`

Now, just because the result is positiv, that does not mean that is the only possible value for a, if you square -4 you can also get 16 as a result, so a can be negative 4 or positive 4:

a=±4

The correct option is B.