Given:
Angle A = 120 degrees
Side opposite angle C = 150 meters
Side opposite angle B = 275 meters
Find:
Angle B
Solution:
Since we have two sides given and an included angle, we can use cosine law.
Let's look for the length of the side opposite Angle A first.
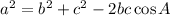
where a = length of the side opposite Angle A or side BC
b = side opposite Angle B or Side AC
c = side opposite Angle C or Side AB
A = Angle A
Since we already have the data above, let's plug it in to the formula we have.
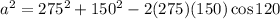
Then, solve a.
![\begin{gathered} a^2=75,625+22,500-82,500(-0.5) \\ a^2=98,125+41,250 \\ a^2=139,375 \\ \sqrt[]{a^2}=\sqrt[]{139,375} \\ a\approx373.3296\approx373.33 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/a2zo4nnec1bvcruuws09jni19a20z4xpei.png)
Hence, the length of side opposite a or Side BC is approximately 373.33 meters.
Now, to solve for Angle B, we can use the sine law.
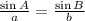
Let's plug in the value of Angle A, side BC or a, and side AC or b to the formula.
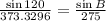
Then, solve for Angle B.

Therefore, the bearing of ship C from ship B is approximately 40 degrees. (rounded off to the nearest degree)