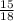Question

Three dice are tossed. what is the probability of rolling 3 different numbers?

Answer 1

Given:Three dice are tossed.

To find: Probability of rolling 3 different numbers.

Let E be the event of getting same number on three dice.

So,the favorable cases for E will be

(1,1,1) , (2,2,2) , (3,3,3), (4,4,4), (5,5,5) , (6,6,6).

So, the number of favorable cases=6

Now,the total number of cases for E will be

`6*6*6`

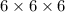
Since each dice has 6 numbers so three dice will have these number of cases.

Now, the probability to have a same number on 3 dice will be

`P(E)=\frac{\text{Number of favorable cases}}{\text{Number of cases}}\text{ }`
`\begin{gathered} P(E)=(6)/(6*6*6) \\ =(1)/(36) \end{gathered}`

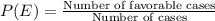
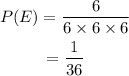
Now, probability of rolling 3 different numbers is

`P(nu\text{mbers are different on thr}ee\text{ dice)}=1-P(E)`
`\begin{gathered} =1-(1)/(36) \\ =(30)/(36) \\ =(15)/(18) \end{gathered}`

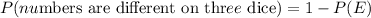
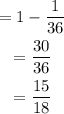
Hence, the probability of rolling three different numbers is

`(15)/(18)`