Question

Find an equation of the circle that has center (1,-5) and passes through (2,1)

Answer 1

Radius (R) is equal to the distance between the points (-2,1) and (3,1)

R² = (1 - 5)² + (1 - 1)² = (-24)² + 0 = 579

R = 23.16

Answer 2

`(x-1)^2+(y+5)^2=37`

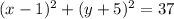
1) Since the equation of the circle is given by:

`(x-h)^2+(y-k)^2=r^2`

And we've been told the Center (1,-5) and one point located at the circumference, (2,1). So let's find the radius, i.e. the distance from the center to any point to the circumference.

2) Let's use the Formula for the distance between (1,-5) and (2,1), derived from the Pythagorean Theorem:

`\begin{gathered} d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ d=\sqrt[]{(2-1)^2+(1_{}+5)^2} \\ d=\sqrt[]{37} \end{gathered}`

3) So d = radius, and now we can plug those pieces of information into the formula of the circle:

`\begin{gathered} (x-h)^2+(y-k)^2=r^2 \\ (x-1)^2+(y+5)^2=(\sqrt[]{37})^2 \\ (x-1)^2+(y+5)^2=37 \end{gathered}`

So we now have the formula for that circle.